Quando ho iniziato a programmare, pensavo che il vero pericolo fosse lo spaghetti code, non la sedia. Ma con il passare dei giorni, mi sono ritrovato intrappolato in una routine fatta di click, bug, caffeina ed empanadas di troppo… e con la schiena sempre più dolorante (“Dal street food al food journal: il mio percorso per cambiare abitudini alimentari”, 2022).

È stato in quel momento che ho iniziato a farmi una domanda tanto semplice quanto fondamentale: quanta energia consuma davvero il mio corpo? 🤨

Per provare a rispondere, avevo persino comprato un Fitbit (“Quantified Self: l’illusione del self-tracking con Fitbit”, 2025). Eppure continuavo a chiedermi: le calorie bruciate🔥 che leggevo sul display erano un dato reale… o solo una stima pensata per rassicurarmi?

Quanta energia consuma il corpo?

Non parlo di diete restrittive o rinunce estreme, ma del desiderio di capire — in modo oggettivo — qual è il mio fabbisogno energetico quotidiano, tenendo conto dell’età, del peso, del livello di attività… e del fatto che passo la maggior parte del tempo seduto davanti a uno schermo.
All’inizio pensavo fosse una curiosità da nerd🤓, ma presto ho scoperto che era tutt’altro che banale. Anzi, era una domanda che si erano posti in molti, ben prima di me. Persino lo scrittore Jonathan Swift (1167-1745) , nel suo celebre 📖 I viaggi di Gulliver (1726), commise un errore comune: immaginò che un uomo dodici volte più grande di uno normale avrebbe dovuto mangiare 1.728 volte di più — perché \(12^3\) fa 1.728.

A differenza della geometria, la biologia non obbedisce a regole lineari: segue logiche tutte sue, come ci ricorda Vaclav Smil nel suo "Size: How It Explains the World" (2023). Il metabolismo non cresce in modo proporzionale alla massa: un concetto che, nel corso della storia, ha affascinato scienziati, fisiologi e studiosi di ogni epoca.

Metabolismo e massa

Nel 1838 Sarrus e Rameaux furono tra i primi a proporre che il metabolismo fosse legato alla superficie corporea, non al peso. L’idea era semplice: gli organismi perdono calore dalla pelle, quindi la quantità di energia necessaria per mantenere il calore doveva dipendere dalla superficie esterna. Pochi anni dopo, nel 1849, Regnault e Reiset osservarono che il metabolismo cresceva più lentamente della massa corporea (M), suggerendo che qualcosa non tornava con la proporzionalità diretta.

Negli anni ’30 del Novecento, Brody e Procter e, nello stesso anno, il biologo svizzero Max Kleiber (1893–1976) portarono avanti studi sul metabolismo basale, ovvero l’energia minima necessaria a un organismo per sopravvivere a riposo.

Analizzando i dati metabolici di diverse specie animali, Kleiber dimostrò che il metabolismo non aumenta in modo proporzionale alla massa corporea (M), come si pensava in precedenza. Se così fosse, infatti, un animale due volte più pesante dovrebbe consumare esattamente il doppio dell’energia: questo sarebbe un rapporto lineare, espresso come:

\[\text{BMR} \propto M^1 \]

Allo stesso modo, l’ipotesi della superficie corporea suggeriva un’esponente di 2/3 (cioè \(M^{0.66}\) ), basata sull’idea che la perdita di calore dipendesse dalla superficie esterna.

Kleiber però scoprì che il metabolismo scala in realtà con l’esponente 0.75:

\[\text{BMR} \propto M^{0.75} \]

Pythonic Way

A volte, tutto ciò che serve per comprendere davvero come funziona la relazione tra metabolismo e massa corporea è un buon grafico e PyCharm aperto. Con poche righe di codice Python possiamo generare un grafico che mette a confronto tre modelli fondamentali.

import numpy as np
import matplotlib.pyplot as plt

plt.style.use('dark_background')

# Mass values (in kg) from 0.01 kg (mouse) to 100,000 kg (whale)
mass_kg = np.logspace(-2, 5, 100)

# Metabolic rate calculations based on different scaling laws
BMR_kleiber = mass_kg ** 0.75
BMR_linear = mass_kg
BMR_surface = mass_kg ** 0.66

# Specific animals for annotation
animals = {
    "Topo": 0.02,
    "Uomo": 70,
    "Balena": 100000
}

# Compute BMR values for the labeled animals
animal_bmrs = {name: mass ** 0.75 for name, mass in animals.items()}

# Plotting
plt.figure(figsize=(10, 6))
plt.loglog(mass_kg, BMR_kleiber, label='Legge di Kleiber (BMR ∝ M^0.75)', linewidth=2, color='cyan')
plt.loglog(mass_kg, BMR_linear, '--', label='Proporzionalità lineare (BMR ∝ M^1)', alpha=0.8, color='orange')
plt.loglog(mass_kg, BMR_surface, ':', label='Superficie corporea (BMR ∝ M^0.66)', alpha=0.8, color='lime')

# Annotate specific animals
colors = ['red', 'yellow', 'magenta']
for i, (name, mass) in enumerate(animals.items()):
    bmr = mass ** 0.75
    plt.plot(mass, bmr, 'o', markersize=8, color=colors[i])
    plt.annotate(name, (mass, bmr), textcoords="offset points", xytext=(10,10), ha='left',
                color='white', fontsize=10, fontweight='bold')

plt.title("Visualizzazione della Legge di Kleiber", fontsize=14, color='white', fontweight='bold')
plt.xlabel("Massa corporea (kg)", color='white', fontsize=12)
plt.ylabel("Metabolismo Basale Relativo (unità arbitrarie)", color='white', fontsize=12)

# Personalizza la legenda
legend = plt.legend(fancybox=True, framealpha=0.9)
legend.get_frame().set_facecolor('black')
for text in legend.get_texts():
    text.set_color('white')

# Personalizza la griglia
plt.grid(True, which="both", ls="--", linewidth=0.5, color='gray', alpha=0.7)

# Personalizza i tick
plt.tick_params(colors='white')

plt.tight_layout()
plt.show()

Nel grafico risultante, possiamo vedere come il metabolismo aumenti con la massa corporea in modo non lineare. Gli animali più grandi consumano più energia in assoluto, ma meno per ogni chilo di peso: ed è proprio questa efficienza crescente che la legge di Kleiber ci aiuta a comprendere.

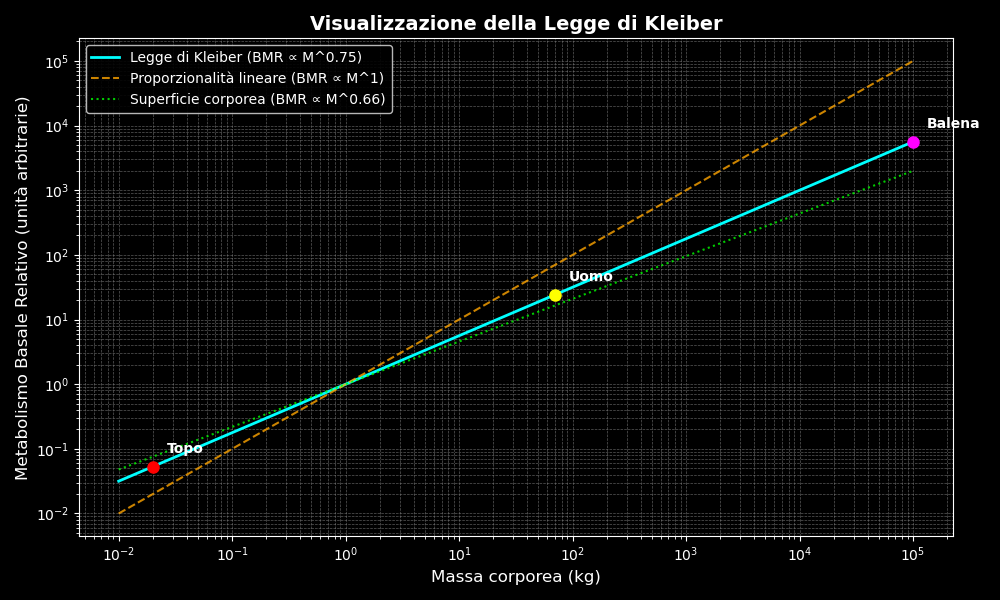
In pochi istanti, la teoria prende forma: dalla balena 🐋(100.000 kg) al topo 🐭(0.02 kg), passando per l’uomo 👨‍🦰(70 kg), la biologia obbedisce a leggi di scala eleganti e misurabili. Ora possiamo vedere chiaramente dove si colloca l’uomo nella scala di Kleiber, tra il topo e la balena. Questo aiuta a visualizzare l’andamento del metabolismo basale su scala logaritmica e quanto meno efficiente diventi (in kcal per kg) all’aumentare della massa.

Il mio posto sulla scala dell'efficienza energetica

La “legge di Kleiber”, discussa in 📖"The Fire of Life: An introduction to animal Energetics" (1975) , mette in luce un principio fondamentale: gli animali più grandi consumano più energia in assoluto, ma meno per unità di massa. In altre parole, sono più efficienti. Un elefante brucia più calorie di un topo, ma per ogni chilo di peso consuma molto meno.

import numpy as np
import matplotlib.pyplot as plt

# Imposta il tema scuro
plt.style.use('dark_background')

# Mass values (in kg) from 0.01 kg (mouse) to 100,000 kg (whale)
mass_kg = np.logspace(-2, 5, 100)

# Metabolic rate calculations based on Kleiber's law
BMR_kleiber = mass_kg ** 0.75

# Specific animals for annotation
animals = {
    "Topo": 0.02,
    "Uomo": 70,
    "Balena": 100000
}

# Calcolo BMR per kg di massa corporea (efficienza metabolica relativa)
BMR_per_kg = BMR_kleiber / mass_kg

# Plotting
plt.figure(figsize=(10, 6))
plt.loglog(mass_kg, BMR_per_kg, color='purple', linewidth=2, label='BMR per kg (BMR/M)')

# Annotazioni per animali
colors = ['red', 'yellow', 'magenta']
for i, (name, mass) in enumerate(animals.items()):
    bmr_per_kg = (mass ** 0.75) / mass
    plt.plot(mass, bmr_per_kg, 'o', markersize=8, color=colors[i])
    plt.annotate(name, (mass, bmr_per_kg), textcoords="offset points", xytext=(10,10), ha='left',
                color='white', fontsize=10, fontweight='bold')

plt.title("Metabolismo Basale per kg di Massa Corporea", fontsize=14, color='white', fontweight='bold')
plt.xlabel("Massa corporea (kg)", color='white', fontsize=12)
plt.ylabel("BMR per kg (unità arbitrarie)", color='white', fontsize=12)

# Personalizza la legenda
legend = plt.legend(fancybox=True, framealpha=0.9)
legend.get_frame().set_facecolor('black')
for text in legend.get_texts():
    text.set_color('white')

# Personalizza la griglia
plt.grid(True, which="both", ls="--", linewidth=0.5, color='gray', alpha=0.7)

# Personalizza i tick
plt.tick_params(colors='white')

plt.tight_layout()
plt.show()

Ecco il grafico che mostra il BMR per kg di massa corporea, ovvero quanta energia consuma ogni chilo di corpo per mantenere le funzioni vitali:

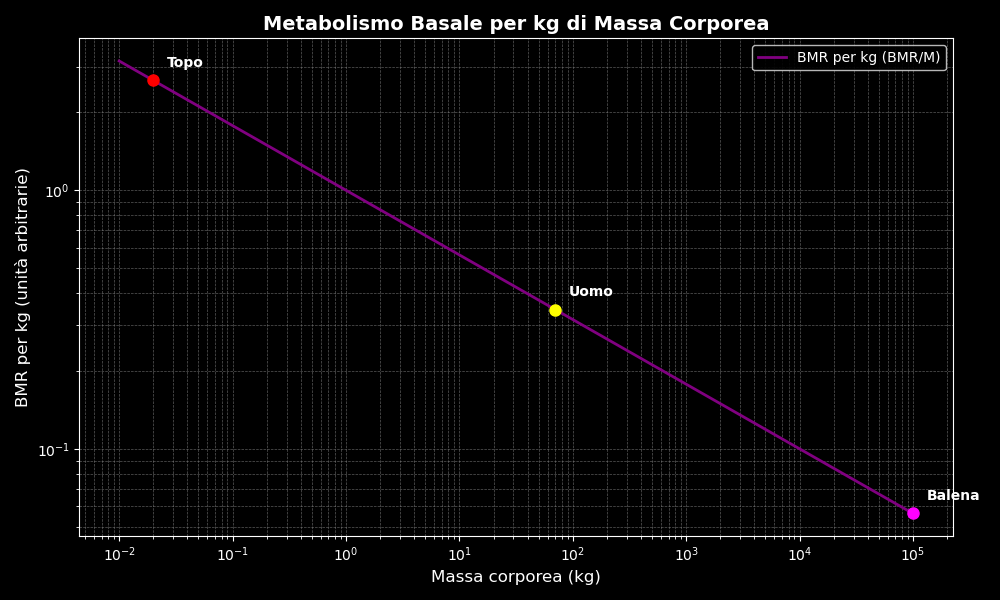
• Il topo 🐭ha un metabolismo per kg molto alto.
• L’uomo 👨‍🦰è nella fascia intermedia.
• La balena 🐋 ha un metabolismo per kg molto più basso, segno di maggiore efficienza energetica.

Questo è il motivo per cui gli animali piccoli "bruciano" più in fretta (devono mangiare spesso), mentre quelli grandi possono sopravvivere più a lungo senza cibo. Adesso sapevo che un uomo adulto consuma meno energia per chilo rispetto a un neonato o a un topo. In un certo senso, avevo trovato il mio posto sulla scala dell’efficienza energetica: tra un topo iperattivo e una balena risparmiatrice.

Codice, bugs ed empanadas

La legge di Kleiber, nata per spiegare le differenze tra specie animali, mi aveva regalato un’intuizione preziosa: il metabolismo non segue una linea retta, ma si adatta in modo intelligente alle dimensioni e alle esigenze di ogni organismo. Finalmente avevo capito perché consumiamo energia in un certo modo — ma restava ancora una domanda aperta, molto più personale: quanta energia consumo davvero, ogni giorno, nella mia routine fatta di codice, bug… y tal vez empanadas? 🤨 Una domanda semplice solo in apparenza. Ma la risposta, come vedremo in un prossimo articolo, è tutt’altro che banale.